SIMCC's Maths Warriors' Challenge
/ 13 min read
Table of Contents
Maths Warriors’ Challenge
Curzon is going to Singapore tomorrow to compete in the Singapore International Math Olympiad Challenge (SIMOC). In addition to the Individual Contest, there’s also apparently a team-based competition called the Maths Warriors’ Challenge.
The SIMCC sent out some preliminary instructions so that everybody can familiarize themselves with the game. So after watching the YouTube tutorial, we decided to play a few rounds. My wife, Curzon, and I each competed in a few rounds, but it only took a couple games for me to notice something concerning: the player to go first was winning. In fact, out of the 7 initial games we played the 1st player won 6 times.
I don’t think this is a sample size issue. While playing as the second player I felt constantly on the back foot and that most of my decisions were essentially forced. On the other hand, as I was back-seating P1’s gameplay it seemed that there was both freedom to make several choices and quite a bit of margin of error.
So I decided to test my theory and code up a quick bot and have it play against itself over and over. Before we get into the results, let’s go over the rules:
The Gameplay
Maths Warrior is a turn-based dice duel game. Players each roll a set of RPG dice (in this case d4, d6, d8, d10, d12, and d20) and use them to attack each other’s dice until one side has no dice left.
Core mechanics:
- Strength attack: Use a die that is equal to or bigger than an opponent’s die to knock it out.
- Mind attack: Combine your dice arithmetically (using addition, subtraction, multiplication, or division) to match the value of a target die.
- Initiative: Both players roll all their dice and sort them from smallest to biggest. The player with the smallest die goes first. If those are tied, compare the next smallest, and so on. If everything ties exactly, P1 goes first by default. To balance this, when only one die remains on each side, the player who went first must beat the last die by a bigger number - a tie favors the second player.
Gameplay loop:
- Players take turns making legal moves.
- After a successful attack, the attacking dice are rerolled.
- If no legal moves exist, the turn passes.
- The last player with dice left wins.
My Claim
SIMCC knows going first helps, so they give the second player a small edge at the very end: if it’s down to one die each, the first player must beat the last die outright - tying isn’t enough. My claim:
- Attacking first gives an enormous advantage, and
- This final-round rule barely matters.
The Test
I wrote a simple Python bot to play this game. The game is so “small” that it doesn’t need any fancy AI or search algorithms. It’s basically a one-ply Monte Carlo simulation:
- On each turn, the bot lists all possible moves (about 200 on the first turn, dropping off quickly as dice are eliminated).
- For each possible move, it simulates the rest of the game 1,000 times using a basic greedy strategy: always attack the opponent’s biggest remaining die first.
- It averages the win rate for every move and picks the one with the best score.
- Then it switches to the next player and repeats this process until someone has no dice left.
- The winner is whoever still has dice in the end.
Clearly this won’t lead to the absolute best, but in practice it performs OK. For example, here’s the output of one random game:
| Turn | Player 1 Dice | Player 2 Dice | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| d4 | d6 | d8 | d10 | d12 | d20 | d4 | d6 | d8 | d10 | d12 | d20 | |
| 1 | 1 | 6 | 3 | 4 | 6 | 6 | 4 | 5 | 3 | 5 | 3 | 18 |
| 2 | 3 | 6 | 1 | 4 | 6 | 9 | 4 | 5 | 3 | 5 | 3 | 0 |
| 3 | 3 | 6 | 1 | 4 | 6 | 0 | 4 | 5 | 6 | 5 | 12 | 0 |
| 4 | 1 | 2 | 3 | 4 | 1 | 0 | 4 | 5 | 6 | 5 | 0 | 0 |
| 5 | 1 | 2 | 3 | 4 | 0 | 0 | 4 | 5 | 6 | 2 | 0 | 0 |
| 6 | 1 | 3 | 8 | 4 | 0 | 0 | 4 | 5 | 6 | 0 | 0 | 0 |
| 7 | 1 | 3 | 8 | 0 | 0 | 0 | 1 | 5 | 6 | 0 | 0 | 0 |
| 8 | 4 | 3 | 1 | 0 | 0 | 0 | 1 | 5 | 0 | 0 | 0 | 0 |
| 9 | 4 | 3 | 0 | 0 | 0 | 0 | 3 | 5 | 0 | 0 | 0 | 0 |
| 10 | 4 | 1 | 0 | 0 | 0 | 0 | 0 | 5 | 0 | 0 | 0 | 0 |
| 11 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 0 |
Just to go over the first few turns:
- P1 used their d4, d8, and d20 to mind attack P2’s d20 (). P1 then rerolled those 3 dice and obtained a 3, 1, and 9 respectively.
- P2 used their d8 and d12 to mind attack P1’s d20 (). P2 then rerolled those 2 dice and obtained a 6 and a 12.
- etc…
Ultimately P2 wins this game because in the final round their 2 is higher than P1’s 1. Note that for this to happen P1 had to roll a 1 for their d8 at the end of turn 7, followed by a 1 on their d6 at the end of turn 9. That is quite difficult to recover from.
The Results
I played 2000 matches and the results are as follows:
| Player | Wins | Winrate (%) |
|---|---|---|
| Player 1 | 1573 | 78.65% |
| Player 2 | 427 | 21.35% |
| Total | 2000 | 100% |
Observations
Greedy
My main takeaway is that the greedy strategy is almost always good enough. From reviewing the game traces, the bot consistently tries to capture the opponent’s largest die first. When it doesn’t, it’s because there simply isn’t a legal move to do so. In those cases, it almost always takes the second-biggest die instead. So in practice, the greedy approach is effective because the game rarely offers better options.
Final Round Player 2 Advantage
I did not notice a statistically significant advantage in the winrates by toggling on and off the P2 final round edge. Looking through the games, it just doesn’t really come up enough for it to be relevant.
Advantage at Round 8
The first-player advantage really shows up at round 8. Earlier in the game - when it’s 4v4, 5v5, or 6v6 - there’s almost always a way to capture the opponent’s most-sided die. Even with 3v3, you can usually find a valid combination to take out a big target.
But by round 8, P2 typically has only 2 dice left while facing 3 targets. At that point, the options dry up fast: it becomes much harder (or outright impossible) to find any legal attack on the opponent’s biggest die. Instead, P2 is forced to settle for a smaller target - or pass entirely. That’s when the game is effectively over. A typical endgame looks like this:
| Turn | Player 1 Dice | Player 2 Dice | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| d4 | d6 | d8 | d10 | d12 | d20 | d4 | d6 | d8 | d10 | d12 | d20 | |
| 7 | 2 | 1 | 6 | 0 | 0 | 0 | 3 | 4 | 3 | 0 | 0 | 0 |
| 8 | 2 | 5 | 6 | 0 | 0 | 0 | 3 | 4 | 0 | 0 | 0 | 0 |
| 9 | 0 | 5 | 6 | 0 | 0 | 0 | 3 | 1 | 0 | 0 | 0 | 0 |
| 10 | 0 | 3 | 6 | 0 | 0 | 0 | 3 | 0 | 0 | 0 | 0 | 0 |
| 11 | 0 | 0 | 6 | 0 | 0 | 0 | 3 | 0 | 0 | 0 | 0 | 0 |
| 12 | 0 | 0 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
- P1 used their d4 and 6 to mind attack P2’s d8 (). P1 then rerolled those 2 dice and obtained a 2 and a 5.
- P2, with only a 3 and 4 remaining, cannot find a way to capture P1’s d8 (a 6 here). They try to fight on by capturing the d4, but the game is statistically a disaster for P2 at this point.
- etc…
Additional Testing
This Round 8 behaviour was intriguing. The game is typically “equal” before that: in other words P1 captures P2’s d20, P2 captures P1’s d20. P1 captures P2’s d12, P2 captures P1’s d12, etc… But finally something starts to happen at round 7 when it’s 3v3 and it becomes more common to not take your opponent’s most-sided die. Can we analyze this in isolation?
Simulation
I (disclaimer: mostly ChatGPT) wrote the following Mathematica code to simulate the probability that a certain number of dice would be able to capture another die of a specified value:
IsTargetPossible[numbers_List, target_Integer] := Module[{operators, allSubsets}, operators = {Plus, Subtract, Times, Divide}; allSubsets = Select[Subsets[numbers], Length[#] > 0 &]; Catch[ Do[Module[{perms = Permutations[subset]}, Do[Module[{opCombos = Tuples[operators, Length[perm] - 1]}, Do[Module[{result}, result = Quiet[Check[ Fold[Function[{acc, pair}, pair[[1]][acc, pair[[2]]]], perm[[1]], Transpose[{ops, Rest[perm]}]], $Failed]]; If[result === target, Throw[True, "found"]]], {ops, opCombos}]], {perm, perms}]], {subset, allSubsets}]; False, "found"]];
HasNumberAtLeastTarget[numbers_List, target_Integer] := AnyTrue[numbers, # >= target &];
MonteCarloTargetProbability[dice_List, target_Integer, iterations_Integer] := Module[{successCount = 0}, Do[Module[{rolls, singleHitQ, comboHitQ},(*Roll each die*) rolls = RandomInteger[{1, #}] & /@ dice; (*Check if any single roll already meets/exceeds target*) singleHitQ = HasNumberAtLeastTarget[rolls, target]; (*If not,check if any combo of rolls can make target*) comboHitQ = False; If[! singleHitQ, comboHitQ = IsTargetPossible[rolls, target];]; If[singleHitQ || comboHitQ, successCount++];], {iterations}]; N[successCount/iterations]]The usage looks something like this:
In[144]:= MonteCarloTargetProbability[{4, 6, 8, 10}, 8, 10000]Out[144]= 0.9934What the above line means is that if you have random d4, d6, d8, and d10 dice, the probability that you’re able to capture your opponents die with a value of 8 is 99.34%. We can use this to generate an entire table of probabilities:
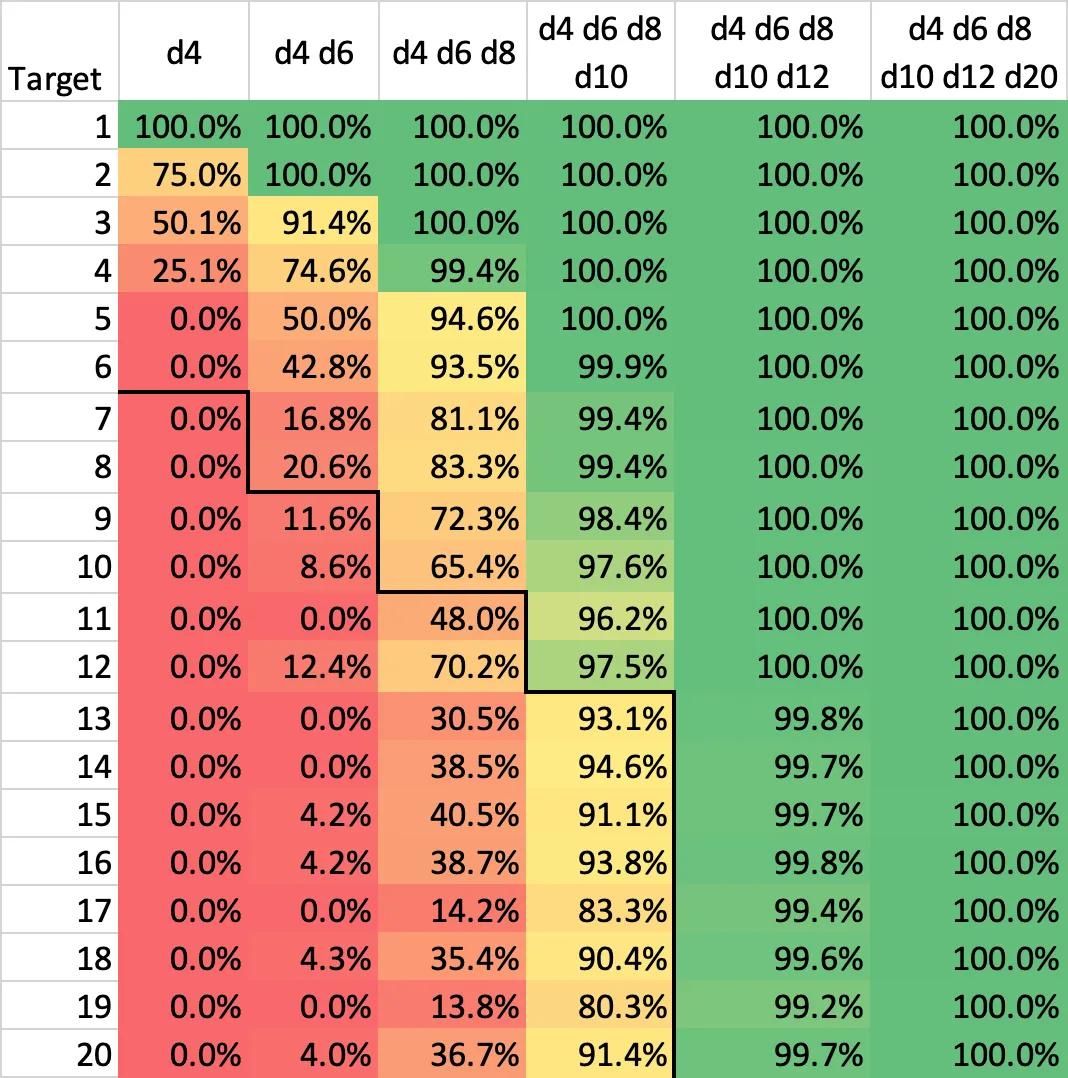
Each row in the table is the value of the target die you’re trying to capture. Each column shows what dice you have left to attack with. For example, the 91.4% in the bottom row means that if you’re trying to capture a die showing 20, and all you have left are your d4, d6, d8, and d10, you still have a 91.4% chance of finding a valid attack to do it.
I’ve added a thick black line to separate out what I’d call the trivial edge cases. Anything below that line is mostly irrelevant - if you’re down to, say, just a d4 and d6 while trying to capture a 20, you’re probably already losing anyway.
Turn-by-Turn Analysis
Most of this is in line with what I suspected except for a few surprising cells which we’ll talk about in a bit. For now, here’s the step-by-step:
- The first four turns are basically freebies - you can almost always capture what you want. There’s only one spot that dips slightly below 97% (to 96.2%): when Player 2 needs to capture Player 1’s d12 showing an 11 on turn 4.
- -
- -
- -
- At 4 dice vs. 4 dice, it’s still a freebie for Player 1. Worst case, Player 2 rolls a 10, and you still have a huge 97.6% chance of capturing it.
- Originally I thought the action started at turn 7, but the analysis indicates that it often starts here. If Player 1’s d10 shows a 7, 8, 9, or 10, Player 2’s chance of capturing it drops to 81.1%, 83.3%, 72.3%, or 65.4% respectively. That’s a significant drop from the near-100% success up to this point.
- We’re “equal” again at d4/d6/d8 vs d4/d6/d8. It’s similar to the above turn except instead of targeting a d10, you will almost certainly only be attacking a d8. Which means instead of facing a 81.1%, 83.3%, 72.3%, or 65.4% chance of success, you are only up against an 81.1%, or 83.3% chance.
- This is where Player 2 gets hammered. If Player 1 can keep their d8 showing a 7 or 8, Player 2’s chance of taking it drops to a miserable 16.8% or 20.6%. If you can’t knock out that die, you’re almost certainly done.
- If Player 2 somehow survives, it’s d4/d6 vs. d4/d6. Now P2 better hope their d6 rolls high; otherwise, P1 finishes the job easily.
- Nothing to analyze from here on out - all of the moves are essentially forced. P2 will try to take P1’s d6 if available, otherwise try the d4. In each situation the 1v1 tiebreaker ensues.
- -
- -
Oddities
For the most part, you want larger dice. Except:
- 7’s are slightly harder to attack than 8’s
- 11’s are slightly harder than 12’s
- 13’s are slightly harder than 14’s, which are slightly harder than 15’s
- 17’s are slightly harder than 18’s
- 19’s are slightly harder than 20’s
In other words, the increased difficulty in strength attacking these numbers is more than offset by the difficulty in reaching them through a mind attack.
Understand that these numbers’ “primeness” also makes them more difficult to mind attack with because of their reduced flexibility with the division operation. I have not analyzed if this offsets the gain from strength attacks and, if not, whether this trade-off is more impactful than their increased defensiveness.
Strategy Implications
I wasn’t expecting to have get a lot of strategy insights from this, but in the end it turned out to be incredibly helpful. Here are my TLDR takeaways:
- The d8/d10 are your bread and butter dice. Prioritize saving them at all costs.
- Do not go out of your way trying to make your d12 or d20 dice larger. Your opponent won’t have trouble capturing them either way.
- An exception to this might be if your opponent is already showing a 7/8 or 9/10 on their d8 or d10 and you need to try to force them to reroll.
- Use the initial freebie turns as “setup turns”. Prioritize rerolling the d8 followed by the d10 to try to get 7/8/9/10.
- Counterintuitively, showing a 20 on the d20 is completely unimportant. Similarly with, say, a 12 on the d12. Do not be afraid to strength attack with those if it means avoiding a mind attack that would reroll your good d8/d10 dice.
- Pray that you get to go first since all of this strategy is dominated by turn order anyway.
Improvements and Further Research
As things stand, I think this game is poorly suited for the SIMOC. If it were just a casual diversion, fine - but there’s an actual award for the teams (randomly assigned) that perform well in Maths Warrior. Worse still, the overall winners for the day are decided by combining each student’s individual results and their Maths Warrior team score.
So your ability to win SIMOC is heavily affected by:
- A game that’s inherently luck-based (dice rolling)
- An advantage determined by a coin flip before the game even starts
- Teams that are randomly assigned by the organizers
That’s frustrating. Especially because there are easy ways to fix the biggest issue: the fact that Player 1 wins ~75% of the time.
The simplest fix? Alternate who goes first and play an even number of rounds per match. Allow a draw to stand as a valid result. This way everyone gets to be Player 1 an equal number of times. Problem solved.
If you really think the starting dice allocation is still too impactful (I don’t), you could improve how you decide who goes first. Instead of using the single lowest die, at least compare the total sum of each player’s dice. It’s totally comical that a player with the holdings will go first against .
Better yet, compare the dice pairwise: d4 vs. d4, d6 vs. d6, etc., and see which player’s set dominates.
I can think of other tweaks too - but I haven’t run the numbers to see how much they’d reduce that lopsided ~75% win rate for Player 1. My guess? Not much. Even in my silly example in the paragraph above, if you start with you can do to capture your opponent’s d20 and trigger a full reroll, which basically cancels out the supposed “disadvantage” that let you go first in the first place.
Or given what we learned today, maybe whoever has the lowest sum of d8 and d10 go first 🙂